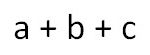Была необходимость в одной работе находить в палитре цвет близкий к заданному. Одним словом, цвет наиболее подходящий для замены текущего. Решение очевидно — надо выбрать точку цветового куба ближайшую к искомой. Также и очевидно решение (Пифагор подсказал):
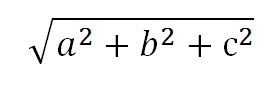 где a, b, c — длины проекций на координатных осях отрезка, соединяющего две точки цветового куба.
где a, b, c — длины проекций на координатных осях отрезка, соединяющего две точки цветового куба.
Можно ли ускорить работу алгоритма?
Если подумать, то вычисление квадратного корня и возведение в степень не требуется. На конечный результат это не повлияет: мы ищем самый короткий отрезок, и работа пойдёт быстрее.
Тогда для нахождения наименьшего отрезка достаточно складывать и сравнивать длины проекций этих отрезков (прости, Пифагор 🙁 ), то есть: